167. 两数之和 II - 输入有序数组
给定一个已按照 升序排列 的整数数组 numbers ,请你从数组中找出两个数满足相加之和等于目标数 target 。
函数应该以长度为 2 的整数数组的形式返回这两个数的下标值。numbers 的下标 从 1 开始计数 ,所以答案数组应当满足 1 <= answer[0] < answer[1] <= numbers.length 。
你可以假设每个输入只对应唯一的答案,而且你不可以重复使用相同的元素。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。示例 2:
输入:numbers = [2,3,4], target = 6
输出:[1,3]示例 3:
输入:numbers = [-1,0], target = -1
输出:[1,2]提示:
2 <= numbers.length <= 3 * 104-1000 <= numbers[i] <= 1000numbers按 递增顺序 排列-1000 <= target <= 1000- 仅存在一个有效答案
解题思路:
很多人做这个题目想不到正确的 O(n)O(n) 解法,即使看了答案理解了,下次再做的时候还是会忘记。要想真正理解这道题,就要明白解法背后的道理。这样不仅可以记住这道题,还能举一反三解决类似的题目。
很多题解只给出了双指针解法的代码,但没有说明解法的正确性。为什么双指针往中间移动时,不会漏掉某些情况呢?要解答这个问题,我们要从缩减搜索空间的角度思考这个解法。下面我将以文字和图片两种方式进行讲解。
需要注意的是,虽然本题叫做 Two Sum II,但解法和 Two Sum 完全不同。
图解双指针解法的原理
在这道题中,我们要寻找的是符合条件的一对下标 (i, j)它们需要满足的约束条件是:
i、j 都是合法的下标,即0 <= i < n, 0 <= j < n
i <j(题目要求)
而我们希望从中找到满足A[i] + A[j] == target **的下标 **(i,j)**。以 **n = 8 为例,这时候全部的搜索空间是:
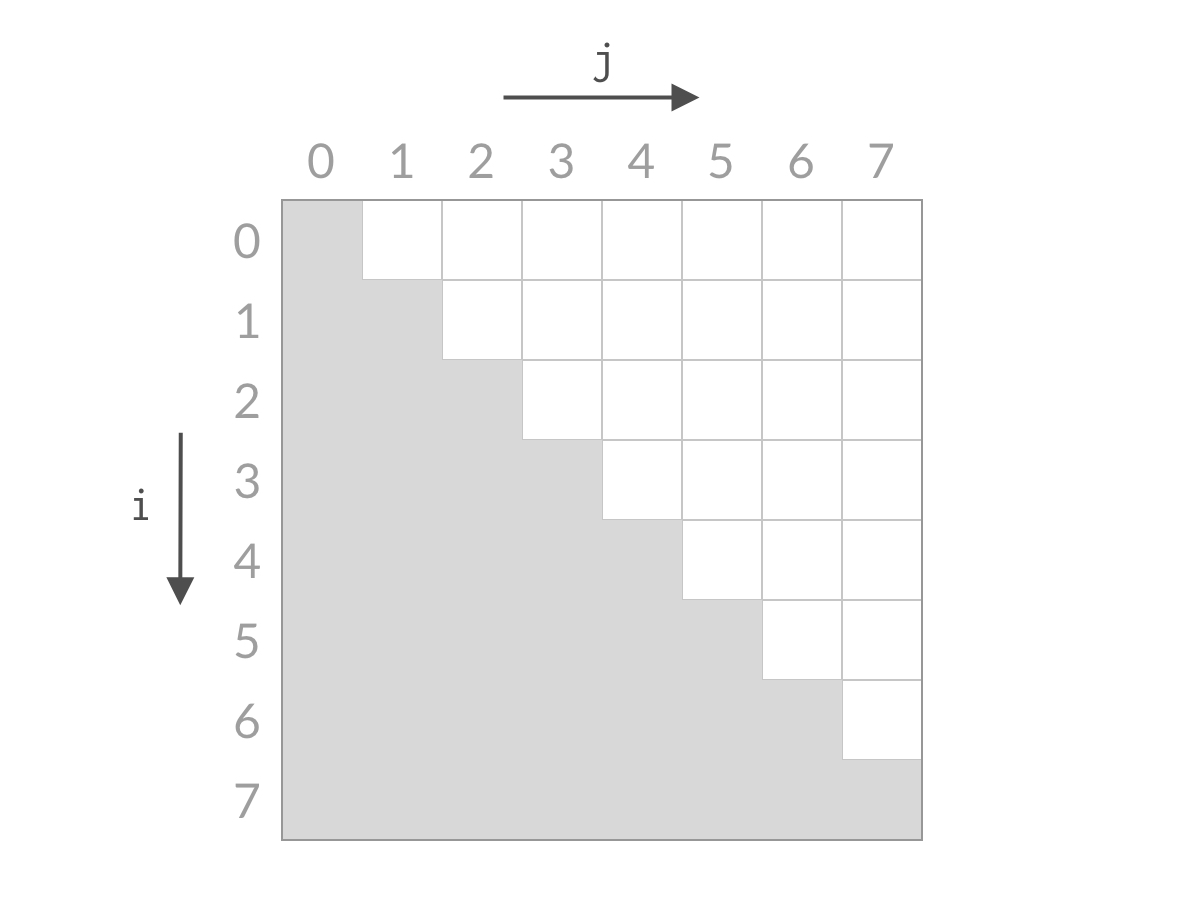
假设此时 A[0] + A[7] 小于 target。这时候,我们应该去找和更大的两个数。由于 A[7] 已经是最大的数了,其他的数跟 A[0] 相加,和只会更小。也就是说 A[0] + A[6] 、A[0] + A[5]、……、A[0] + A[1] 也都小于 target,这些都是不合要求的解,可以一次排除。这相当于 i=0i=0 的情况全部被排除。对应用双指针解法的代码,就是 i++,对应于搜索空间,就是削减了一行的搜索空间,如下图所示。
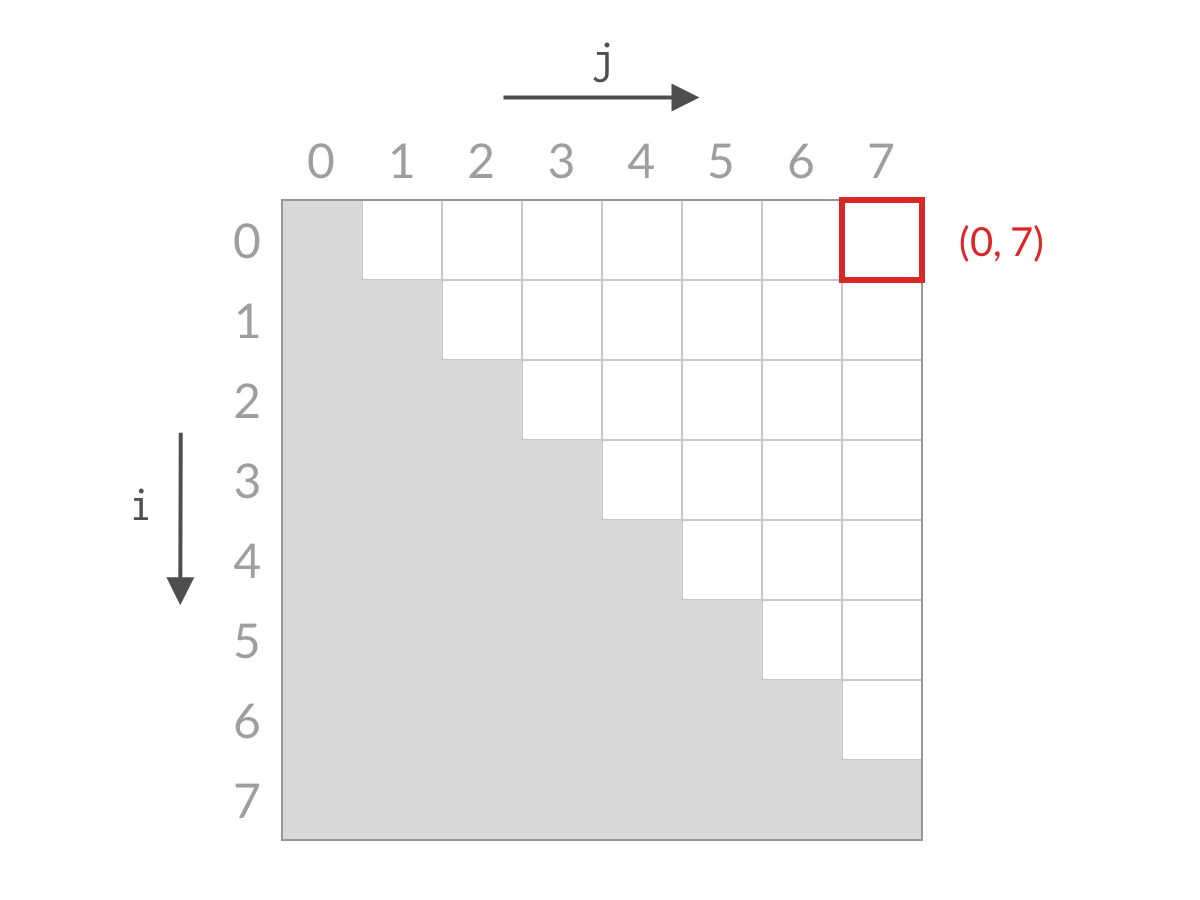
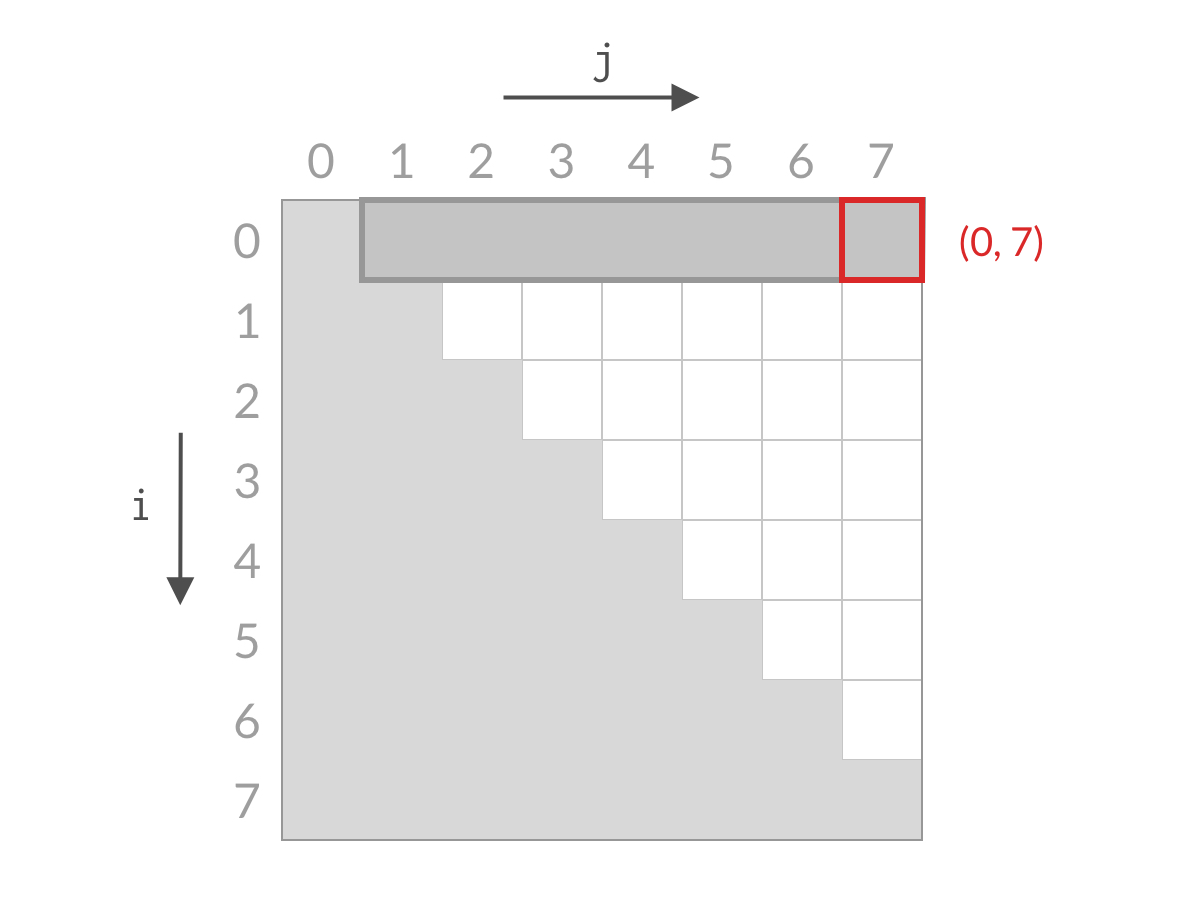
排除掉了搜索空间中的一行之后,我们再看剩余的搜索空间,仍然是倒三角形状。我们检查右上方的单元格 (1, 7)(1,7),计算 A[1] + A[7] 与 target 进行比较。
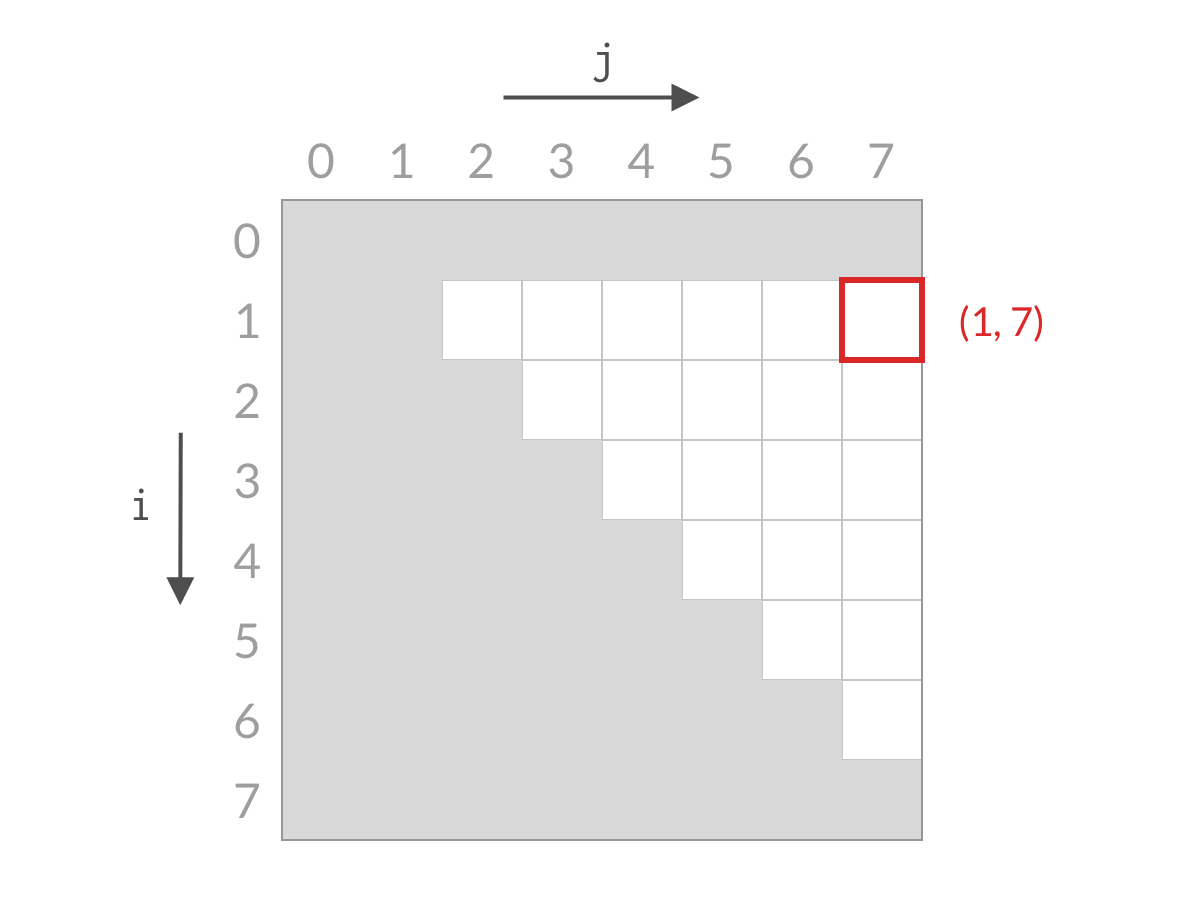
假设此时 A[0] + A[7] 大于 target。这时候,我们应该去找和更小的两个数。由于 A[1] 已经是当前搜索空间最小的数了,其他的数跟 A[7] 相加的话,和只会更大。也就是说 A[1] + A[7] 、A[2] + A[7]、……、A[6] + A[7] 也都大于 target,这些都是不合要求的解,可以一次排除。这相当于 j=0j=0 的情况全部被排除。对应用双指针解法的代码,就是 j++,对应于搜索空间,就是削减了一列的搜索空间,如下图所示。
可以看到,无论 A[i] + A[j] 的结果是大了还是小了,我们都可以排除掉一行或者一列的搜索空间。经过 nn 步以后,就能排除所有的搜索空间,检查完所有的可能性。搜索空间的减小过程如下面动图所示:
> 题解
因为数组已经排好序,我们可以采用方向相反的双指针来寻找这两个数字,一个初始指向最
小的元素,即数组最左边,向右遍历;一个初始指向最大的元素,即数组最右边,向左遍历。
如果两个指针指向元素的和等于给定值,那么它们就是我们要的结果。如果两个指针指向元
素的和小于给定值,我们把左边的指针右移一位,使得当前的和增加一点。如果两个指针指向元
素的和大于给定值,我们把右边的指针左移一位,使得当前的和减少一点。
可以证明,对于排好序且有解的数组,双指针一定能遍历到最优解。证明方法如下:假设最
优解的两个数的位置分别是 l 和 r。我们假设在左指针在 l 左边的时候,右指针已经移动到了 r;
此时两个指针指向值的和小于给定值,因此左指针会一直右移直到到达 l。同理,如果我们假设
在右指针在 r 右边的时候,左指针已经移动到了 l;此时两个指针指向值的和大于给定值,因此
右指针会一直左移直到到达 r。所以双指针在任何时候都不可能处于 (l,r) 之间,又因为不满足条
件时指针必须移动一个,所以最终一定会收敛在 l 和 r。
class Solution {
public:
vector<int> twoSum(vector<int>& num, int t)
{
int n=num.size();
int l=0,r=n-1;
for(int i=0;i<n;++i)
{
int sum=num[l]+num[r];
if(t==sum) break;
if(t>sum) ++l;
else --r;
}
return vector<int> {l+1,r+1};
}
};


