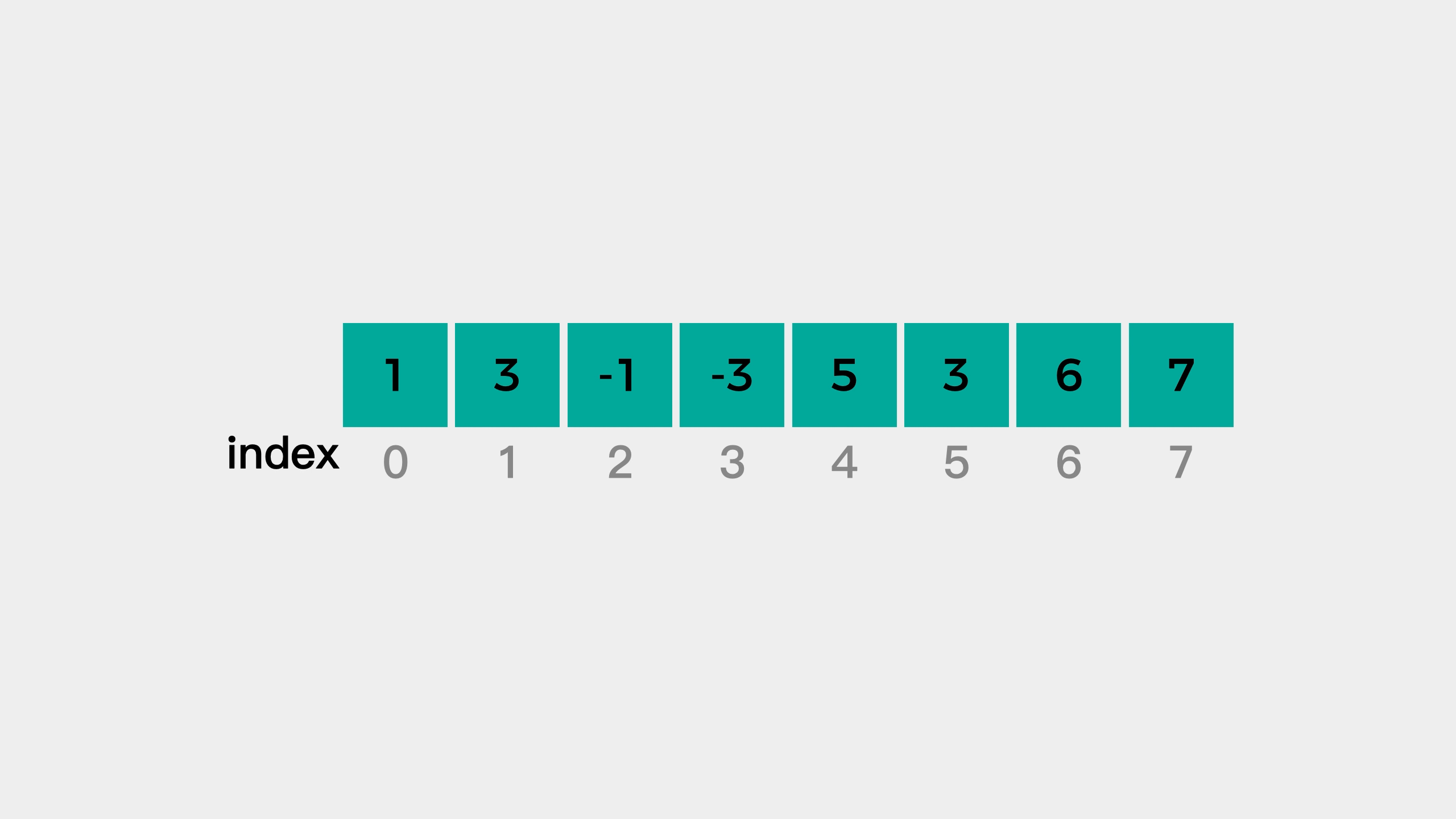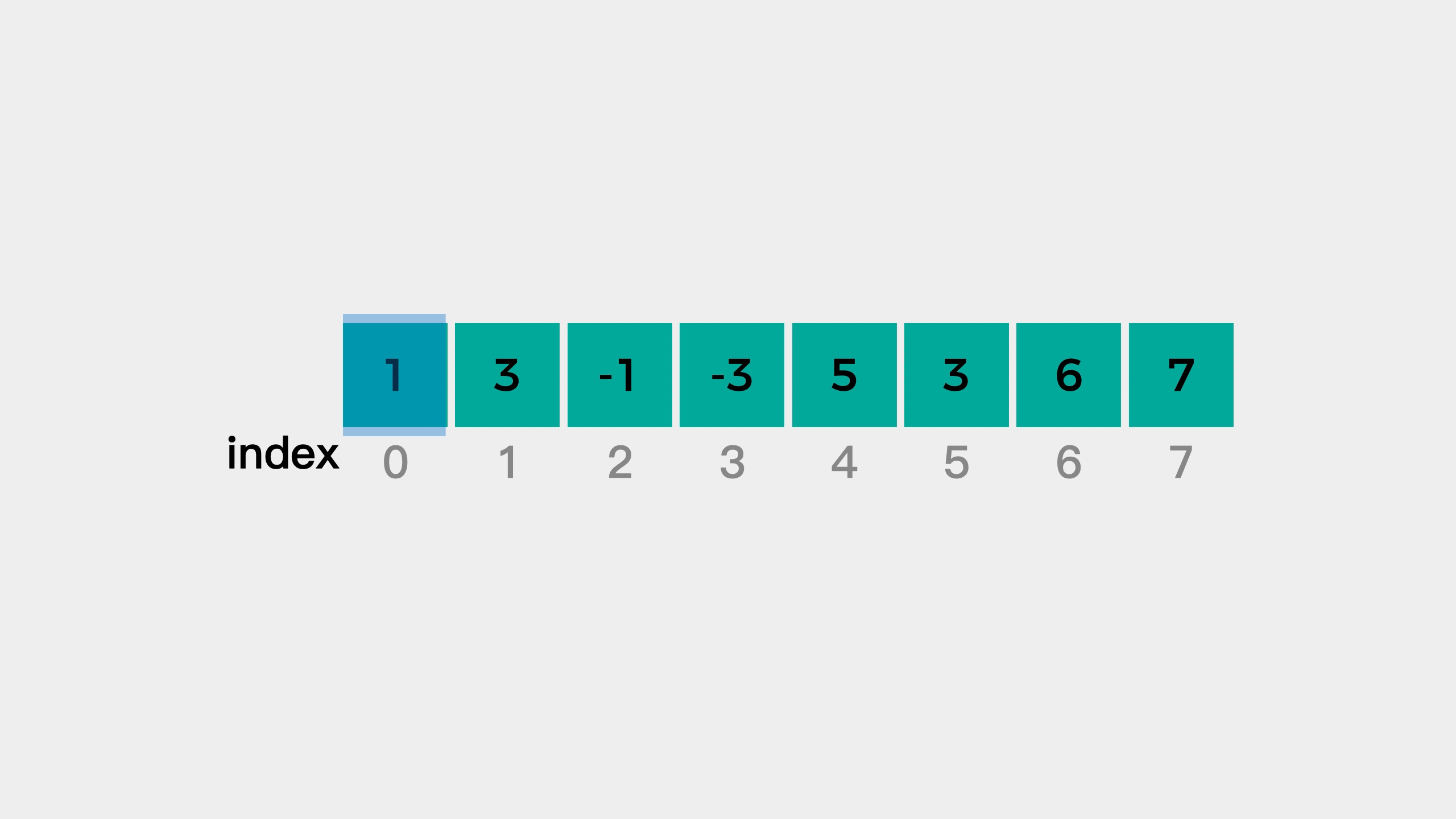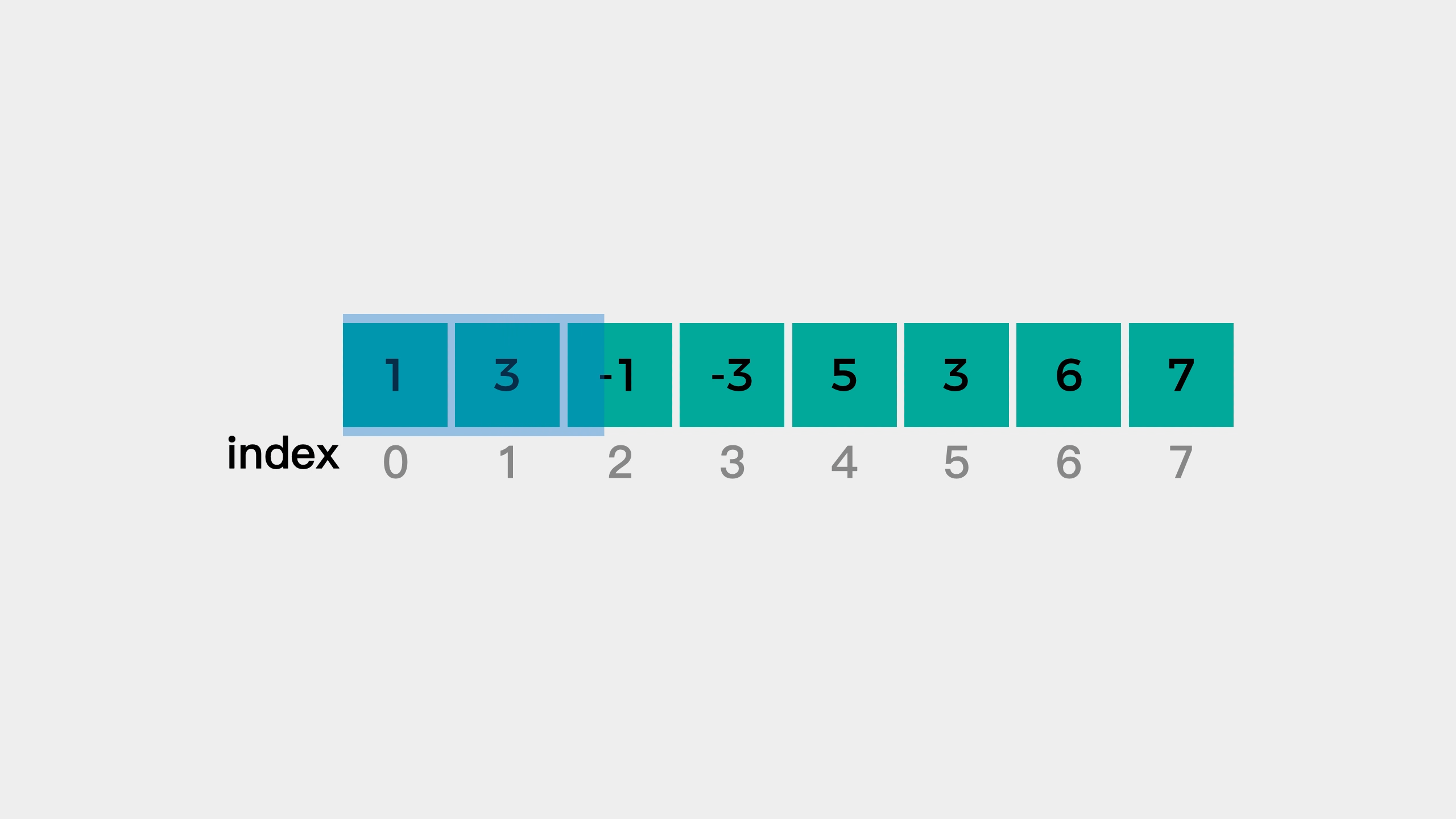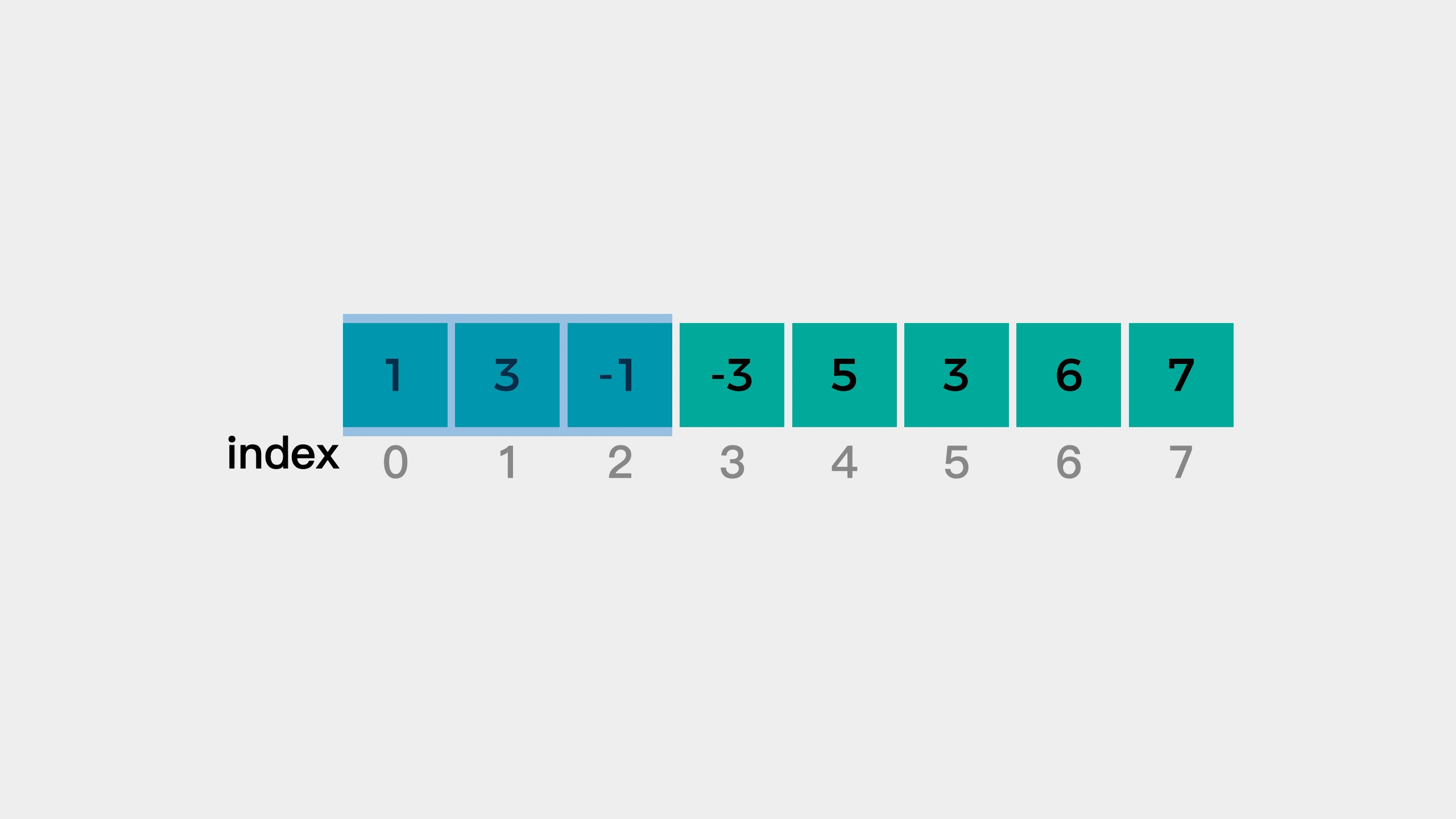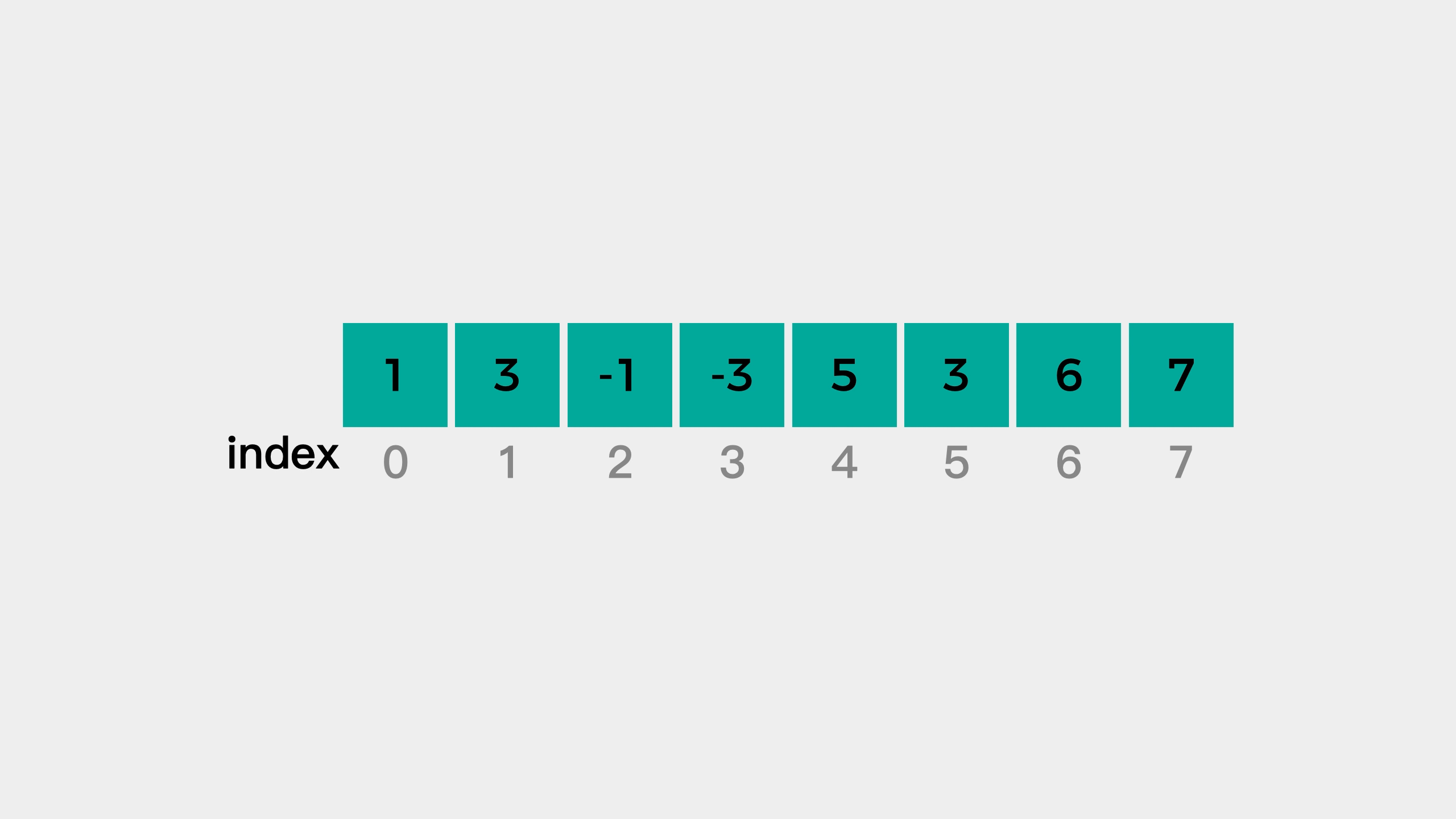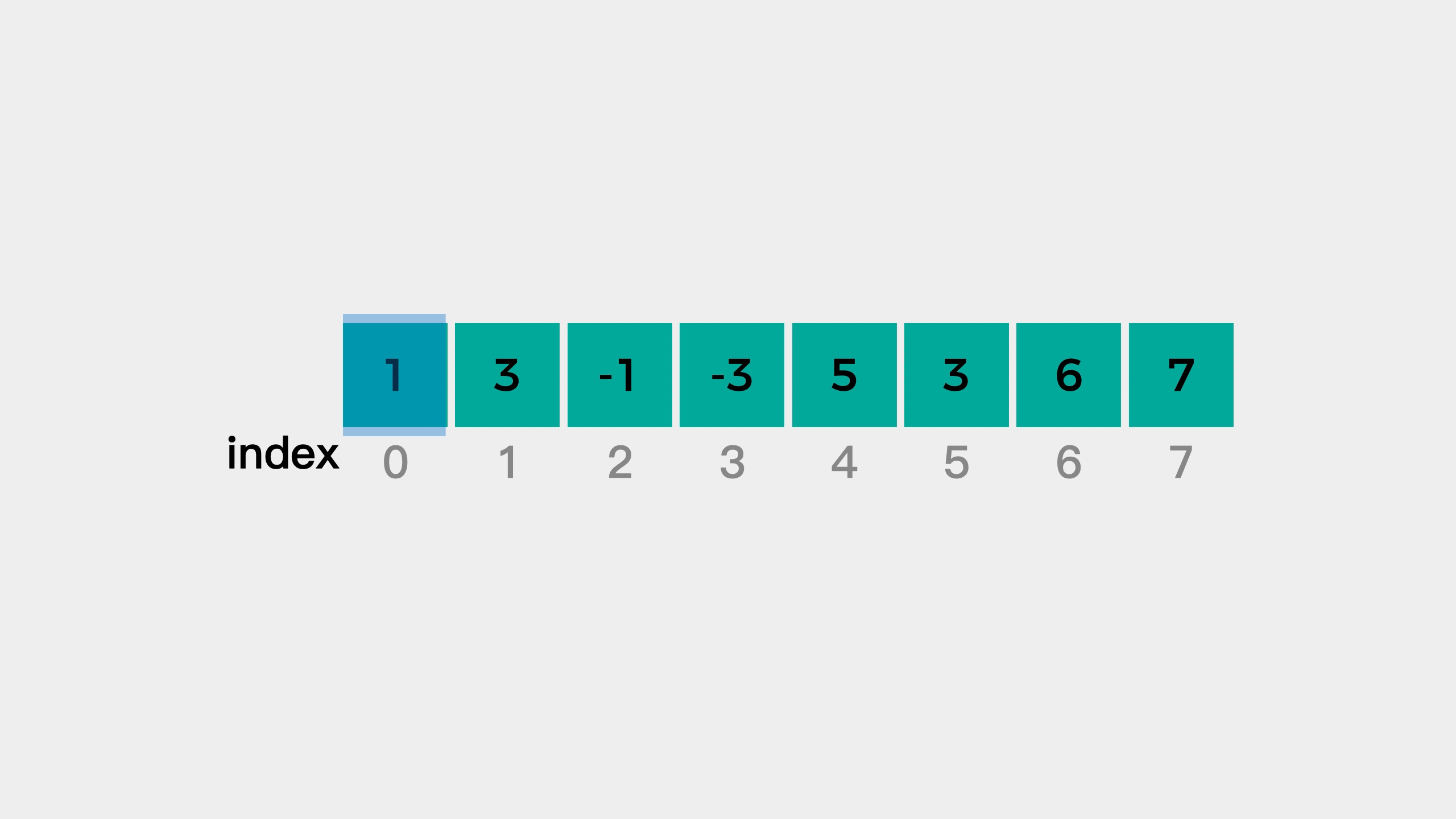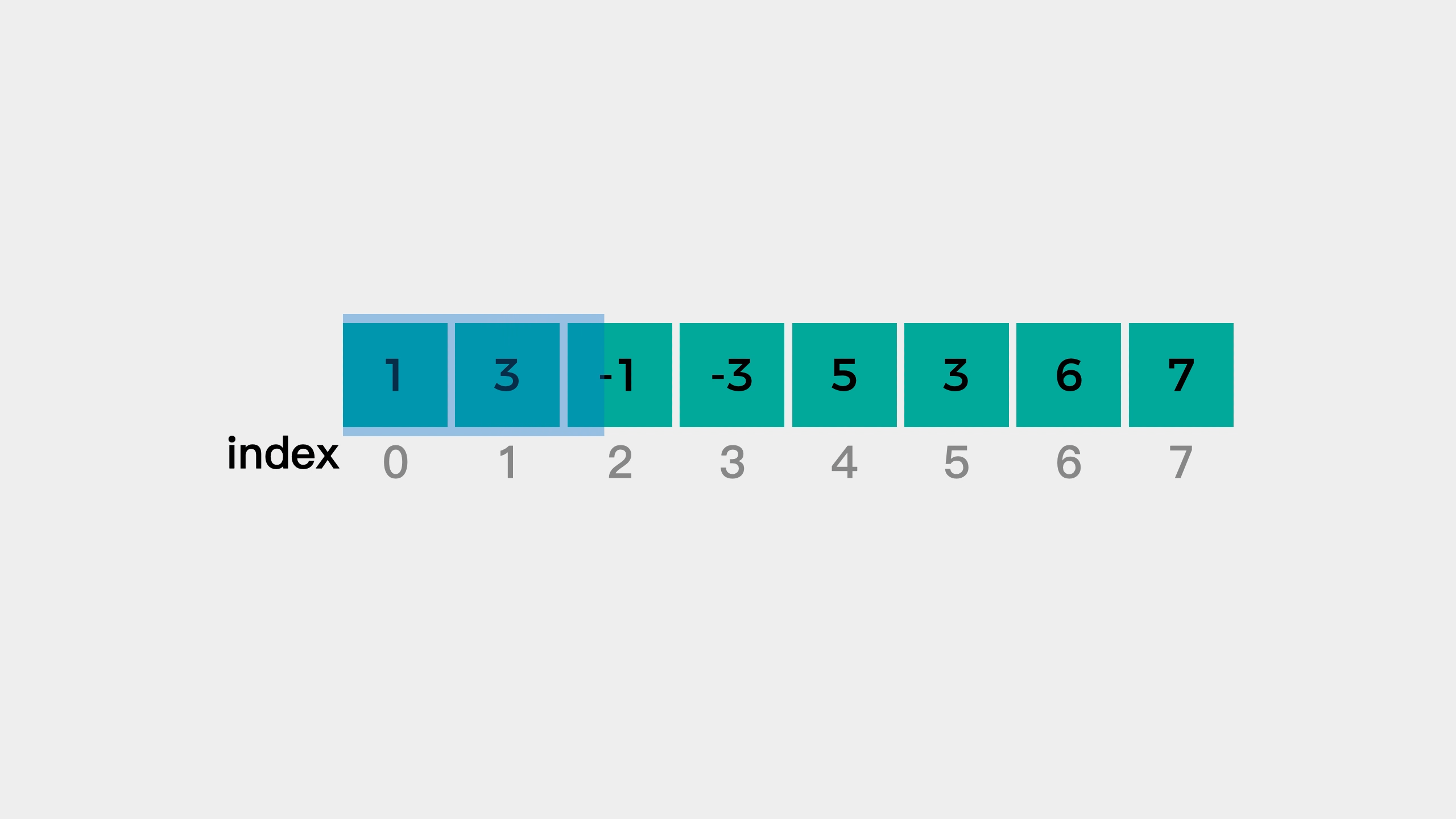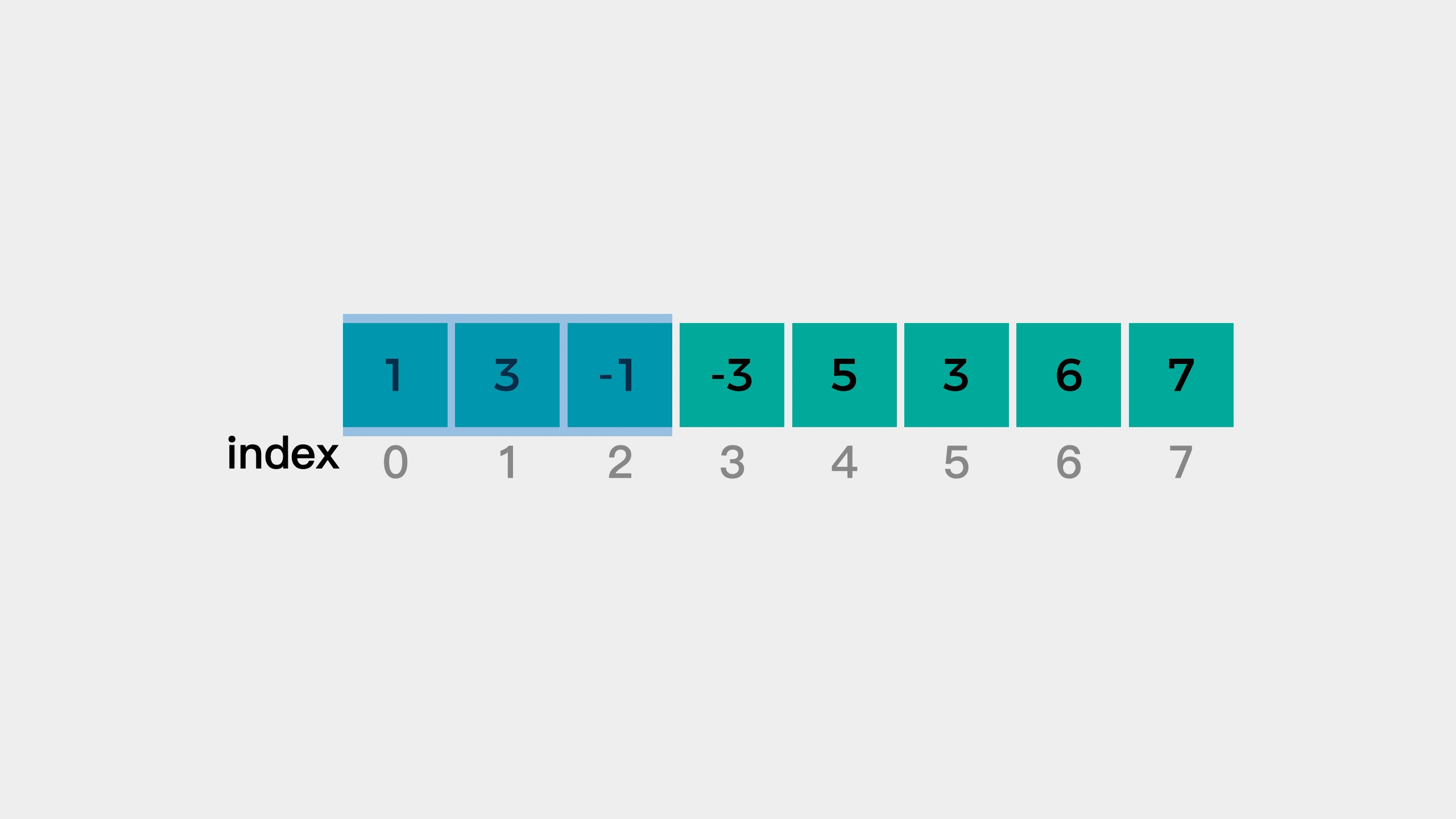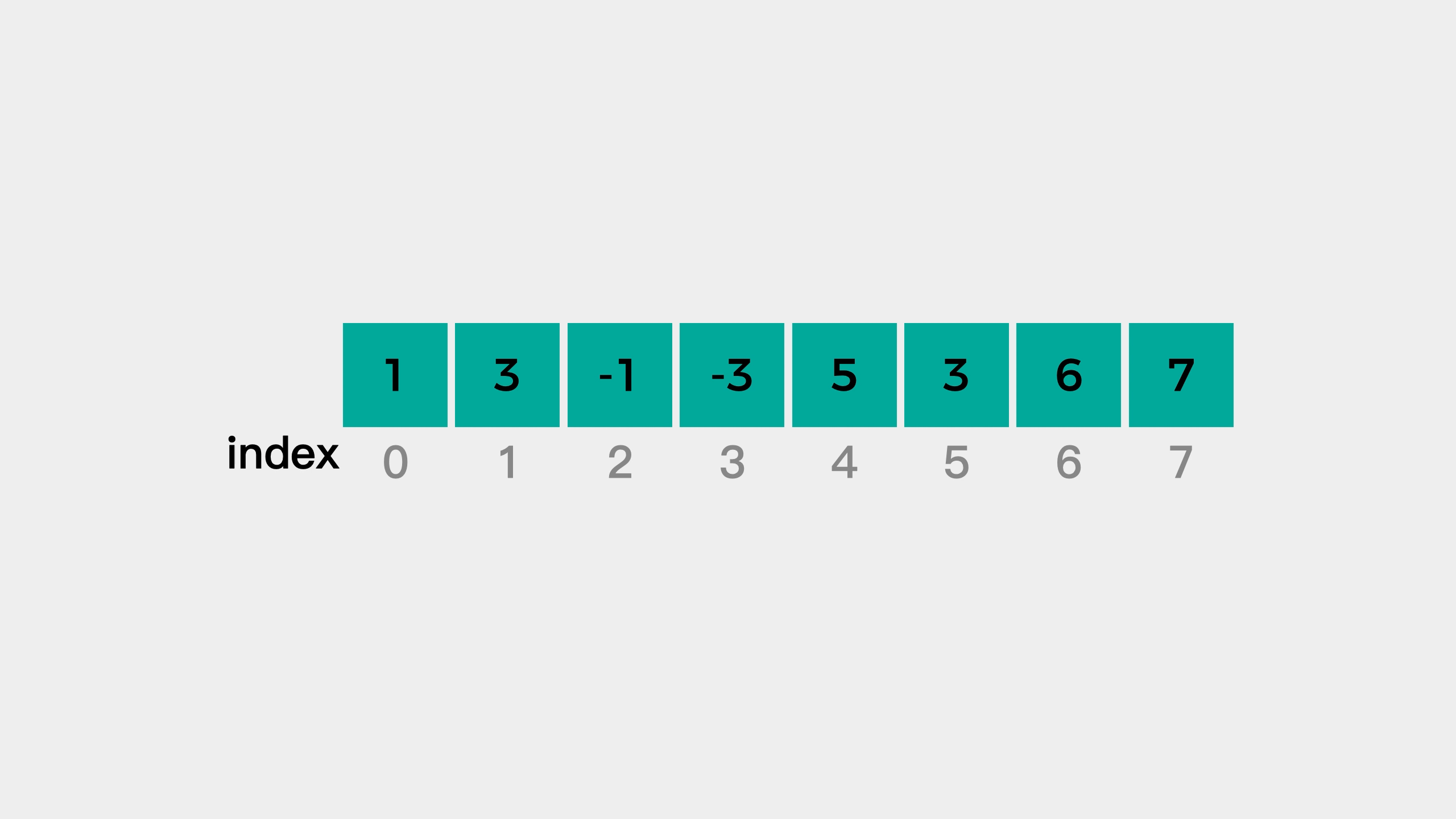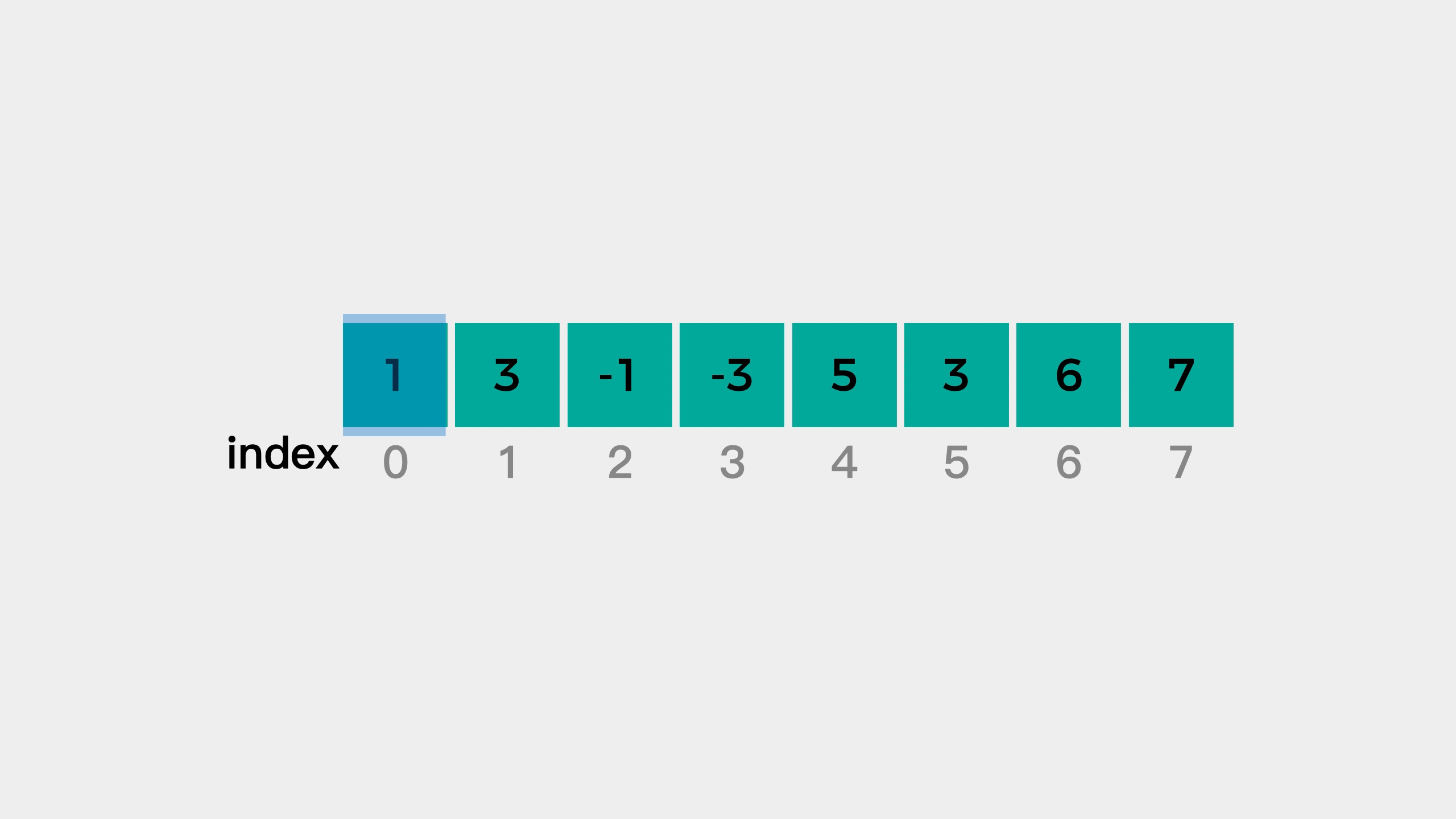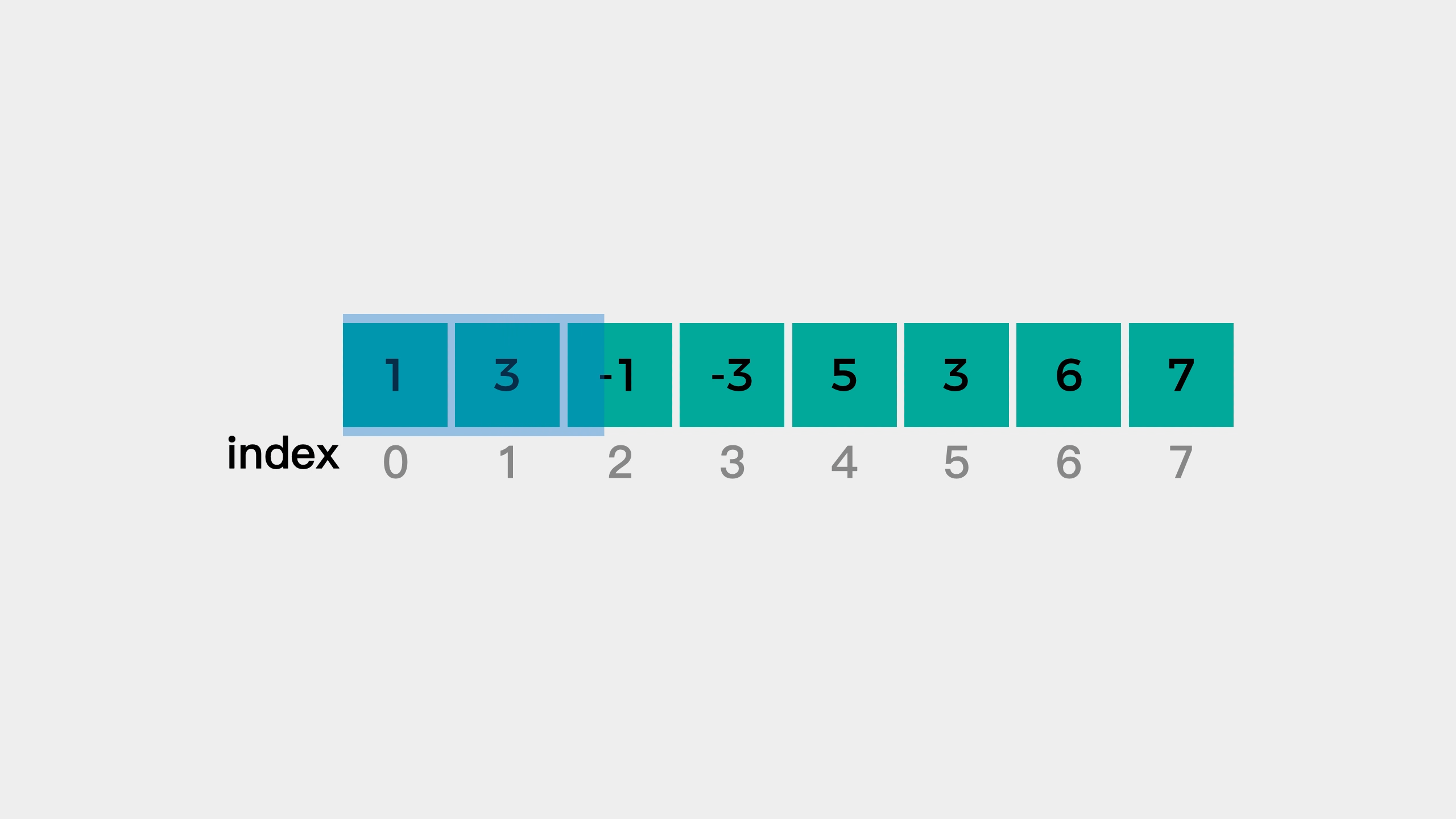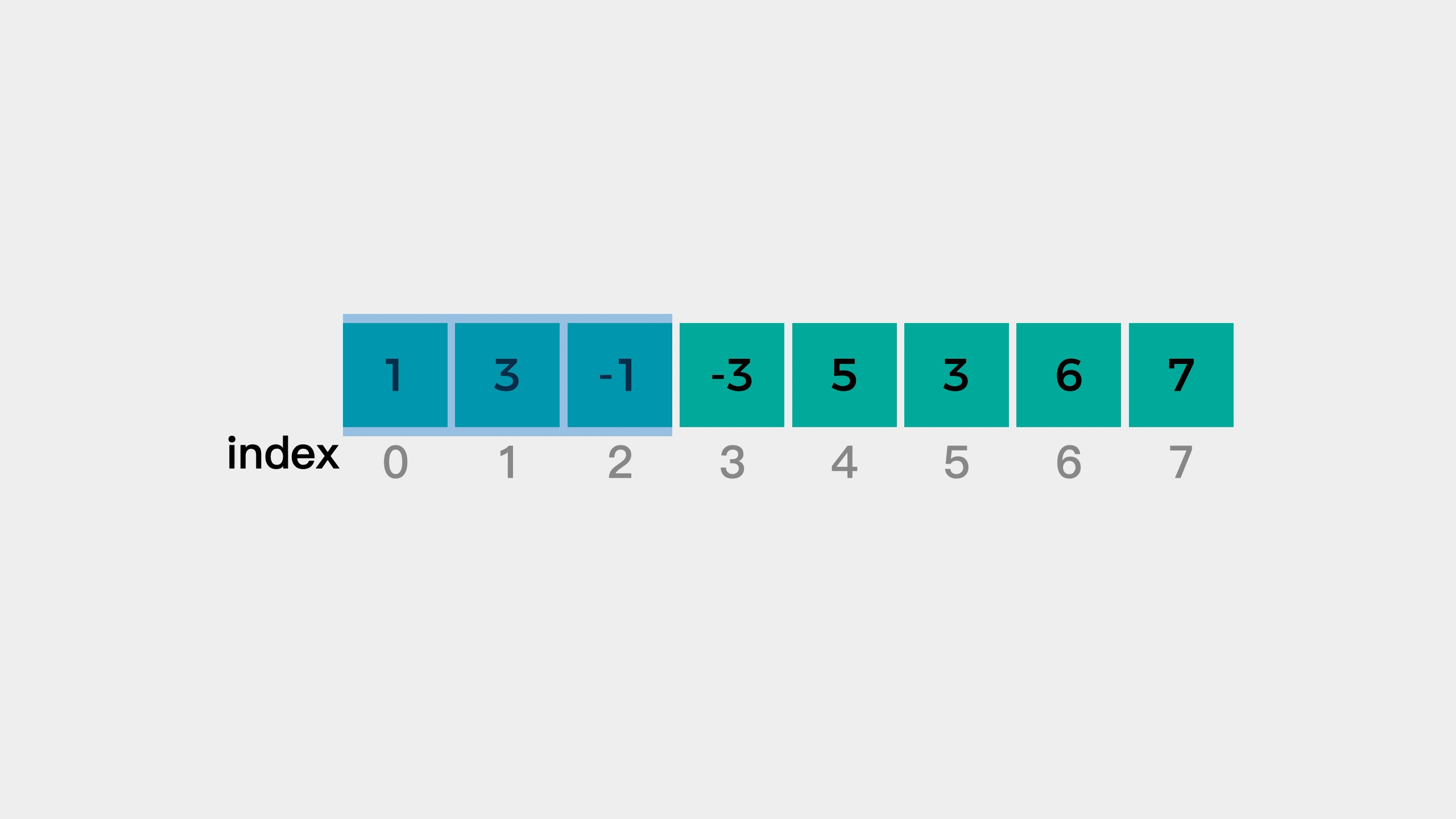Leetcode 239. 滑动窗口最大值
给你一个整数数组 nums,有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。
返回滑动窗口中的最大值。
示例 1:
输入:nums = [1,3,-1,-3,5,3,6,7], k = 3
输出:[3,3,5,5,6,7]
解释:
滑动窗口的位置 最大s值
--------------- -----
[1 3 -1] -3 5 3 6 7 3
1 [3 -1 -3] 5 3 6 7 3
1 3 [-1 -3 5] 3 6 7 5
1 3 -1 [-3 5 3] 6 7 5
1 3 -1 -3 [5 3 6] 7 6
1 3 -1 -3 5 [3 6 7] 7
示例 2:
输入:nums = [1], k = 1
输出:[1]
示例 3:
输入:nums = [1,-1], k = 1
输出:[1,-1]
示例 4:
输入:nums = [9,11], k = 2
输出:[11]
示例 5:
输入:nums = [4,-2], k = 2
输出:[4]
提示:
1 <= nums.length <= 105
-104 <= nums[i] <= 104
1 <= k <= nums.lengthclass Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
int n=nums.size();
vector<int> pre(n),tail(n);
for(int i=0;i<n;++i)
{
if(i%k==0)
pre[i]=nums[i];
else
pre[i]=max(pre[i-1],nums[i]);
}
for(int i=n-1;i>=0;--i)
{
if(i== n-1 || (i+1)%k==0)
tail[i]=nums[i];
else
tail[i]=max(tail[i+1],nums[i]);
}
vector<int> ams;
for(int i=0;i<=n-k;++i)
{
ams.push_back(max(tail[i],pre[i+k-1]));
}
return ams;
}
};class duilie
{
public:
deque<int> data;
void Push(int n)
{
while(!data.empty() && data.back() < n)
data.pop_back();
data.push_back(n);
}
int Max()
{
return data.front();
}
void Pop(int n)
{
if(!data.empty() && data.front() ==n)
data.pop_front();
}
};
class Solution {
public:
vector<int> maxSlidingWindow(vector<int>& nums, int k)
{
duilie dan;
int n=nums.size();
vector<int> s;
for(int i=0;i<n;++i)
{
if(i<k-1)
dan.Push(nums[i]);
else
{
dan.Push(nums[i]);
s.push_back(dan.Max());
dan.Pop(nums[i-k+1]);
}
}
return s;
}
};
思路
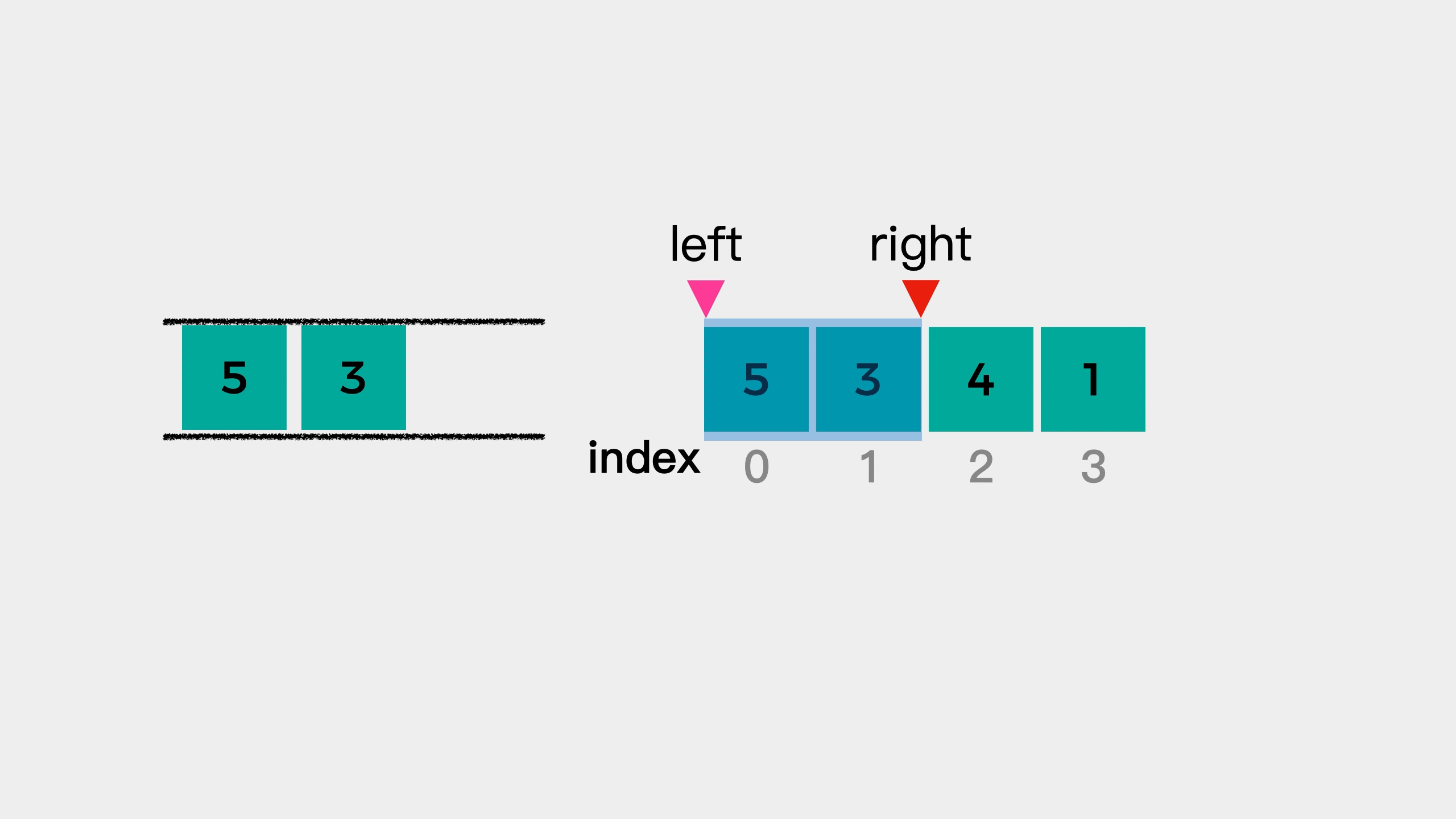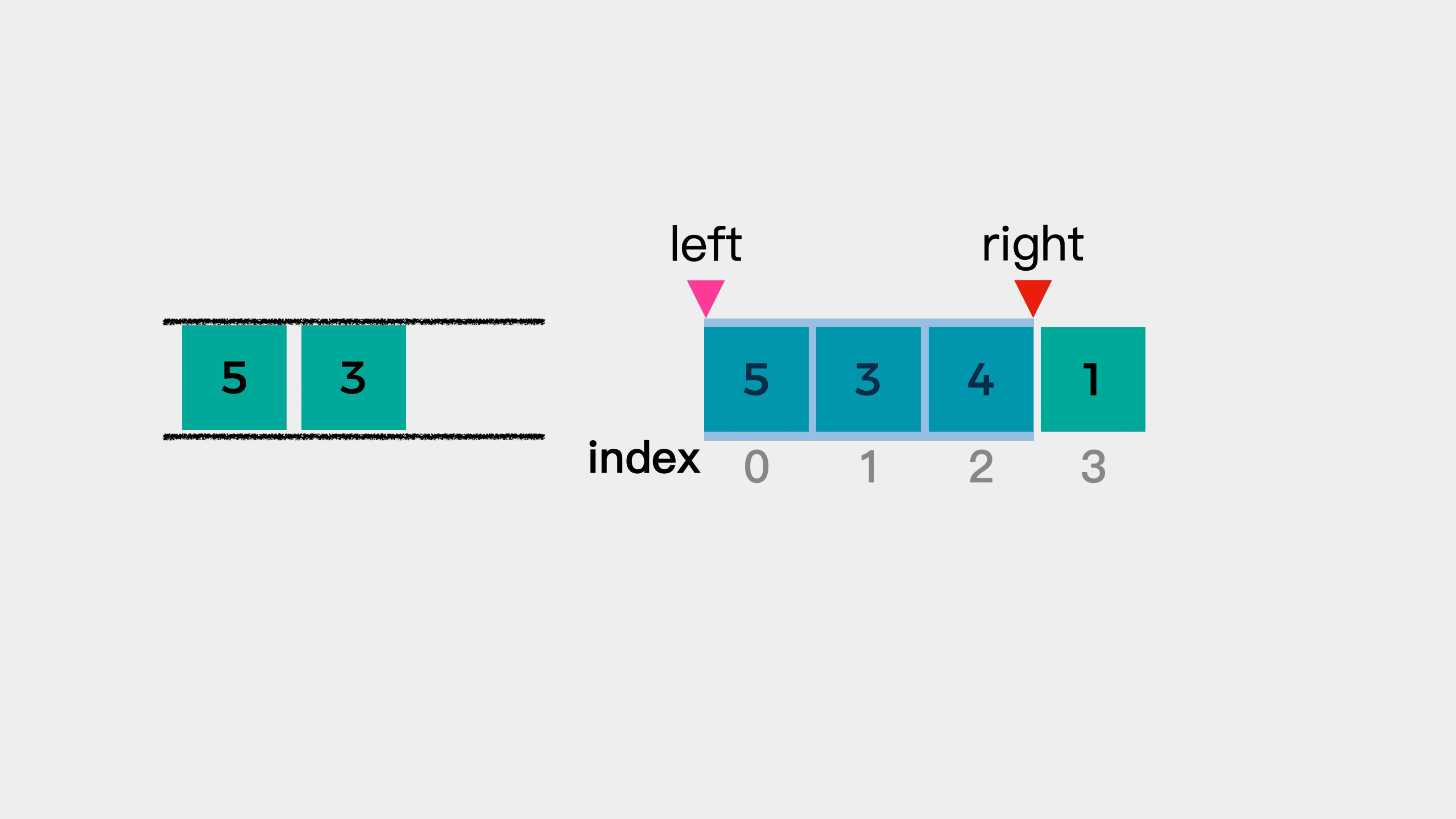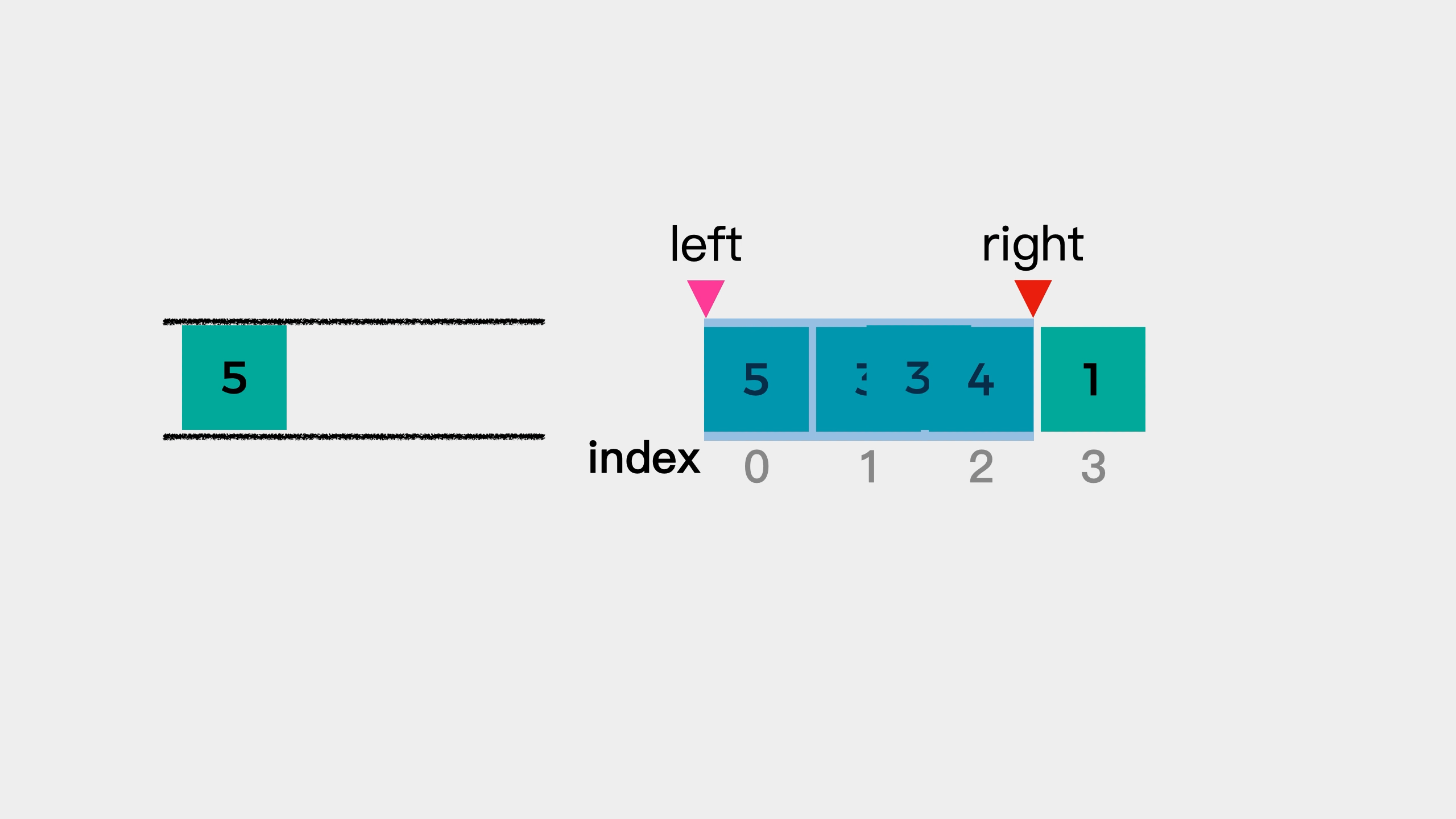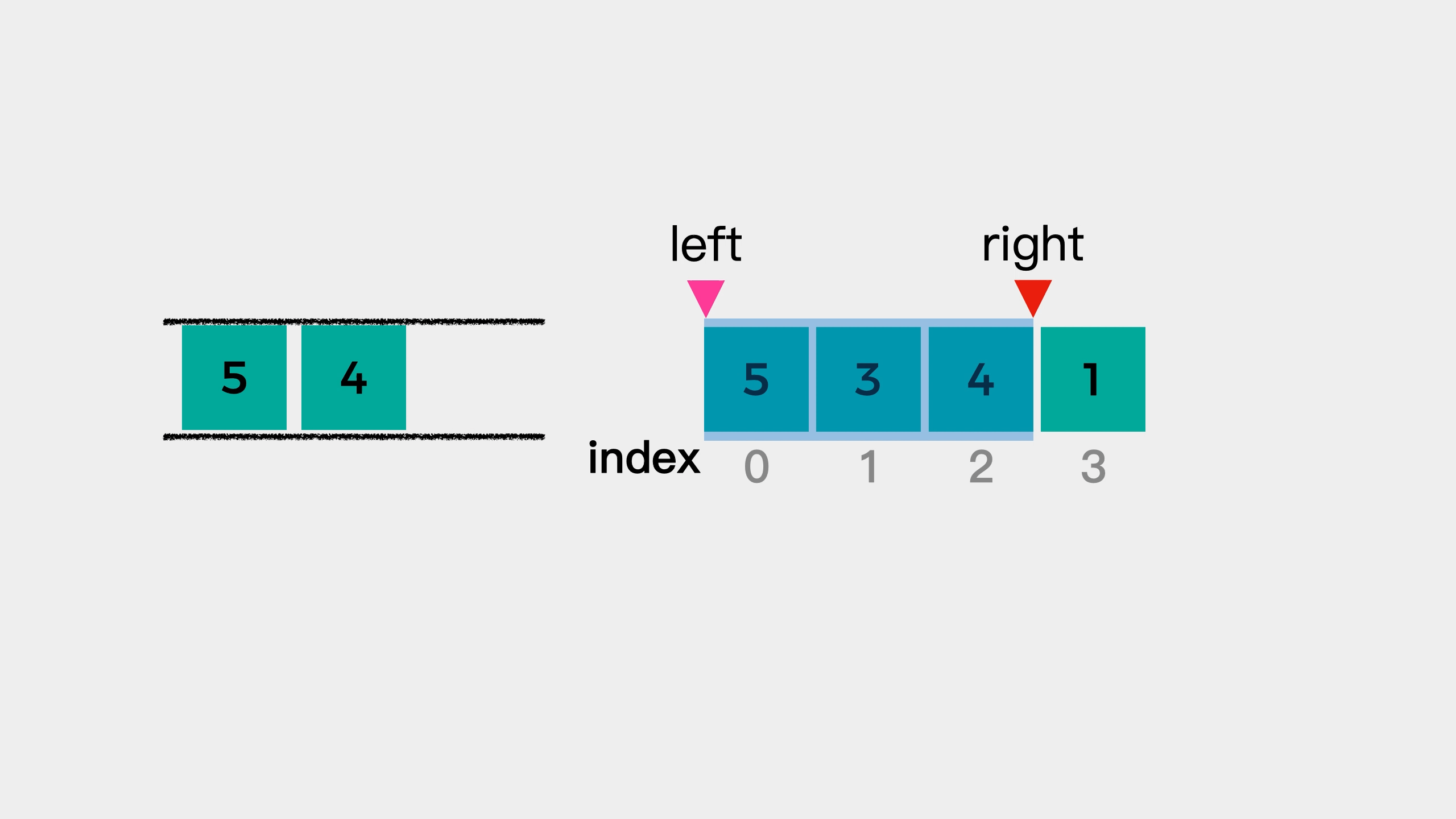
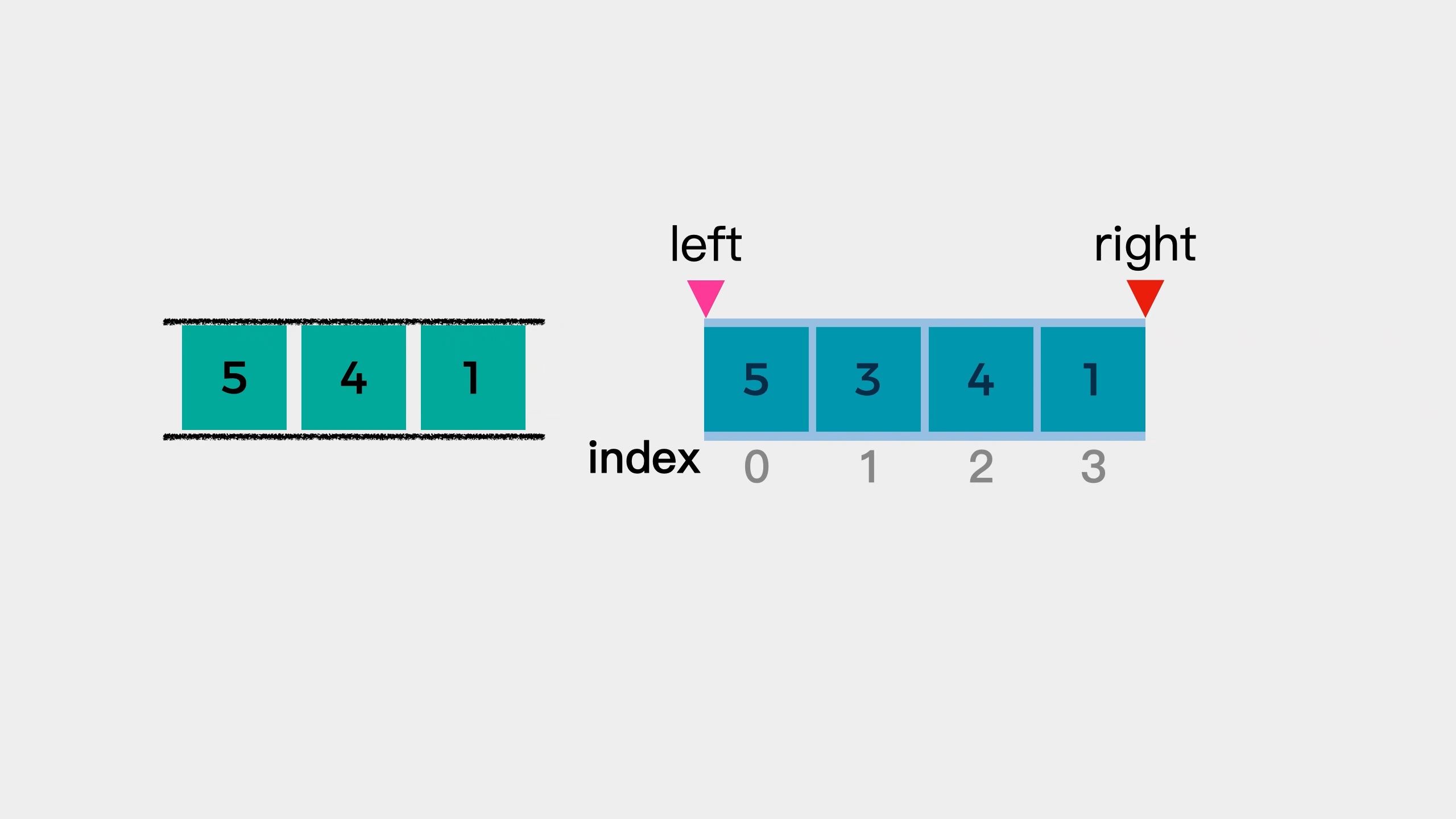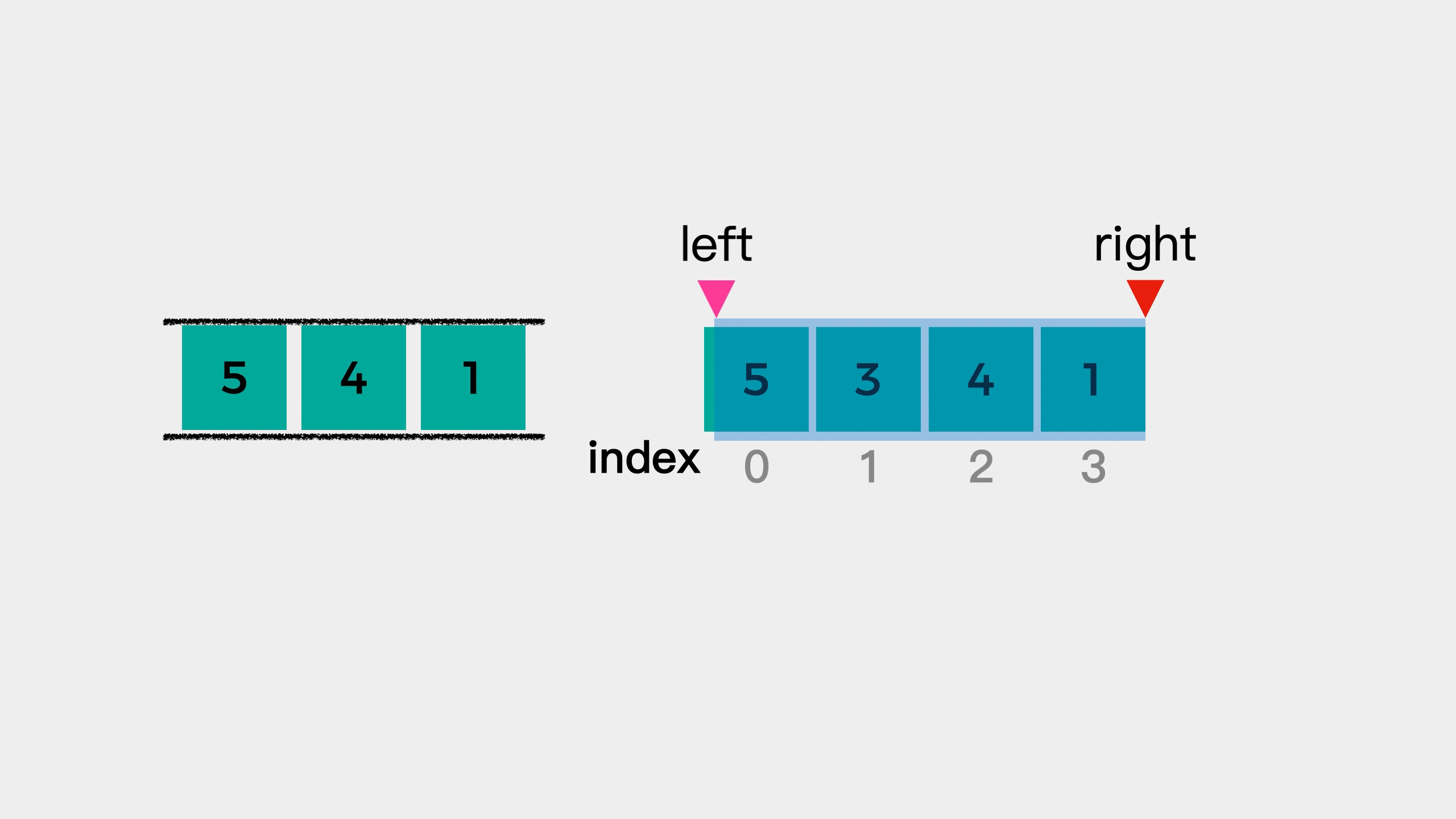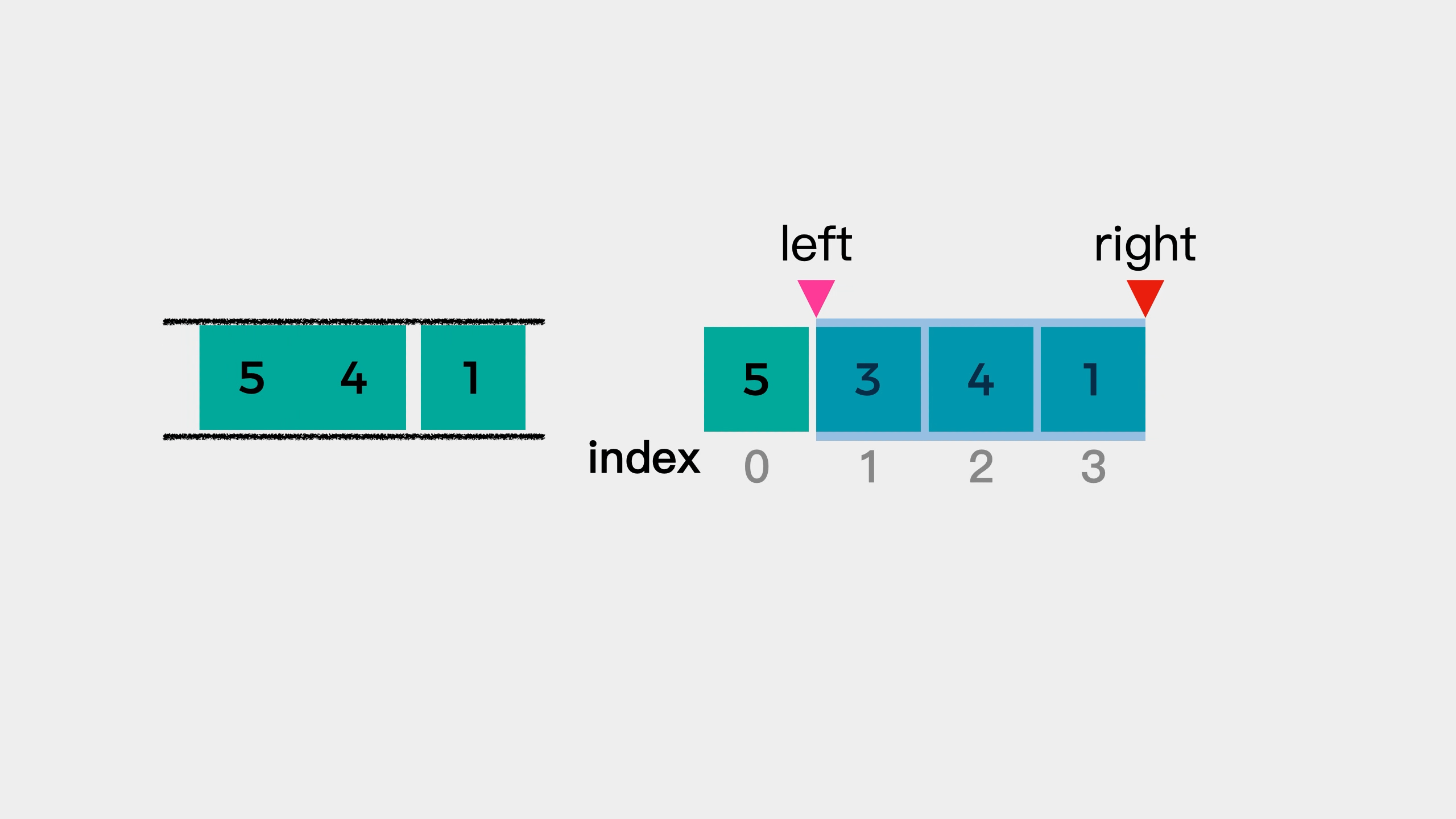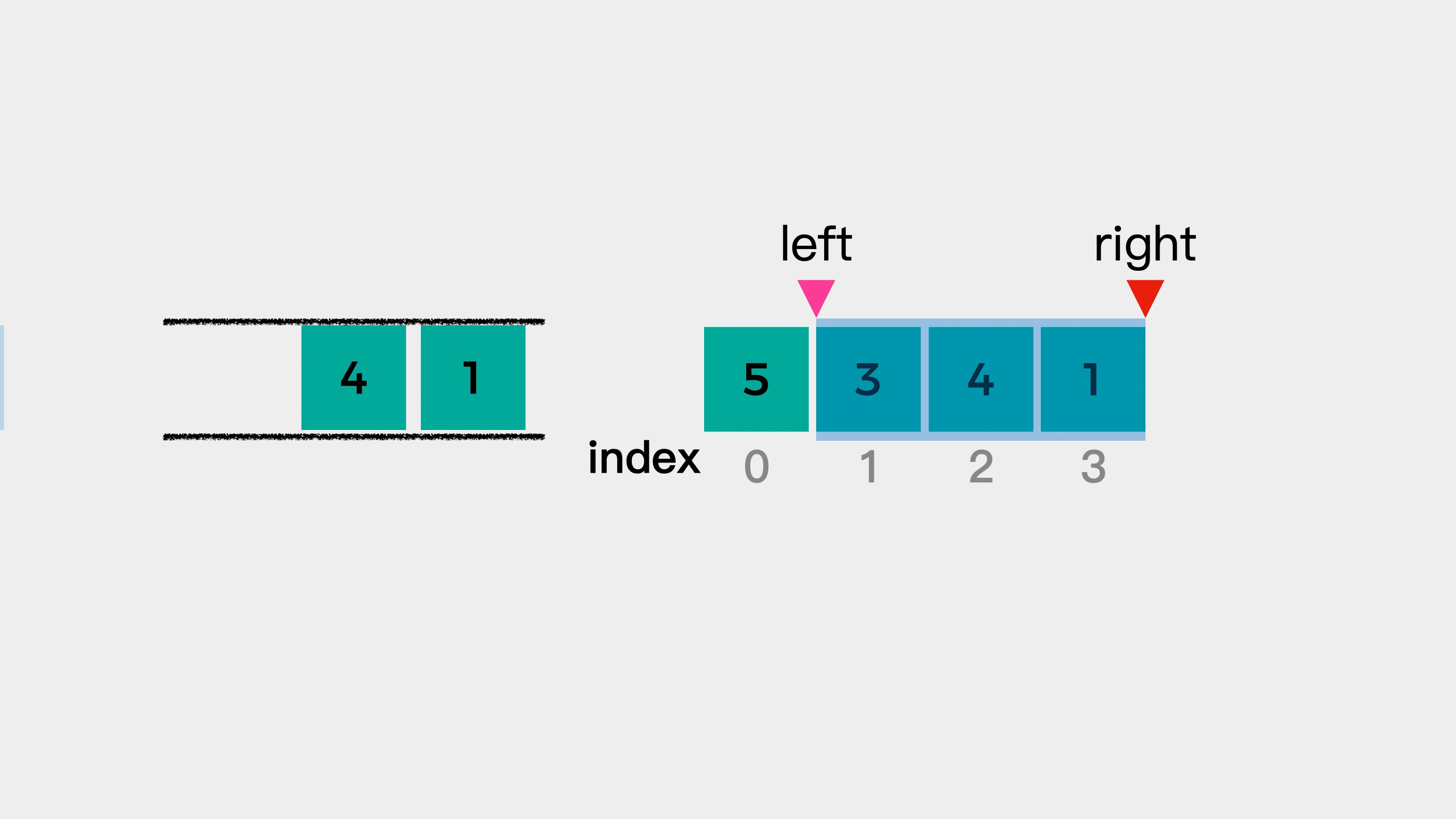
遍历数组,将 数 存放在双向队列中,并用 L,R 来标记窗口的左边界和右边界。队列中保存的并不是真的 数,而是该数值对应的数组下标位置,并且数组中的数要从大到小排序。如果当前遍历的数比队尾的值大,则需要弹出队尾值,直到队列重新满足从大到小的要求。刚开始遍历时,L 和 R 都为 0,有一个形成窗口的过程,此过程没有最大值,L 不动,R 向右移。当窗口大小形成时,L 和 R 一起向右移,每次移动时,判断队首的值的数组下标是否在 [L,R] 中,如果不在则需要弹出队首的值,当前窗口的最大值即为队首的数。
示例
输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3
输出: [3,3,5,5,6,7]
解释过程中队列中都是具体的值,方便理解,具体见代码。
初始状态:L=R=0,队列:{}
i=0,nums[0]=1。队列为空,直接加入。队列:{1}
i=1,nums[1]=3。队尾值为1,3>1,弹出队尾值,加入3。队列:{3}
i=2,nums[2]=-1。队尾值为3,-1<3,直接加入。队列:{3,-1}。此时窗口已经形成,L=0,R=2,result=[3]
i=3,nums[3]=-3。队尾值为-1,-3<-1,直接加入。队列:{3,-1,-3}。队首3对应的下标为1,L=1,R=3,有效。result=[3,3]
i=4,nums[4]=5。队尾值为-3,5>-3,依次弹出后加入。队列:{5}。此时L=2,R=4,有效。result=[3,3,5]
i=5,nums[5]=3。队尾值为5,3<5,直接加入。队列:{5,3}。此时L=3,R=5,有效。result=[3,3,5,5]
i=6,nums[6]=6。队尾值为3,6>3,依次弹出后加入。队列:{6}。此时L=4,R=6,有效。result=[3,3,5,5,6]
i=7,nums[7]=7。队尾值为6,7>6,弹出队尾值后加入。队列:{7}。此时L=5,R=7,有效。result=[3,3,5,5,6,7]
通过示例发现 R=i,L=k-R。由于队列中的值是从大到小排序的,所以每次窗口变动时,只需要判断队首的值是否还在窗口中就行了。
解释一下为什么队列中要存放数组下标的值而不是直接存储数值,因为要判断队首的值是否在窗口范围内,由数组下标取值很方便,而由值取数组下标不是很方便。
代码Java
class Solution {
public int[] maxSlidingWindow(int[] nums, int k) {
if(nums == null || nums.length < 2) return nums;
// 双向队列 保存当前窗口最大值的数组位置 保证队列中数组位置的数值按从大到小排序
LinkedList<Integer> queue = new LinkedList();
// 结果数组
int[] result = new int[nums.length-k+1];
// 遍历nums数组
for(int i = 0;i < nums.length;i++){
// 保证从大到小 如果前面数小则需要依次弹出,直至满足要求
while(!queue.isEmpty() && nums[queue.peekLast()] <= nums[i]){
queue.pollLast();
}
// 添加当前值对应的数组下标
queue.addLast(i);
// 判断当前队列中队首的值是否有效
if(queue.peek() <= i-k){
queue.poll();
}
// 当窗口长度为k时 保存当前窗口中最大值
if(i+1 >= k){
result[i+1-k] = nums[queue.peek()];
}
}
return result;
}
}