链表中环的入口结点
给定一个链表,若其中包含环,则输出环的入口节点。
若其中不包含环,则输出`null`。
#### 样例
```c++
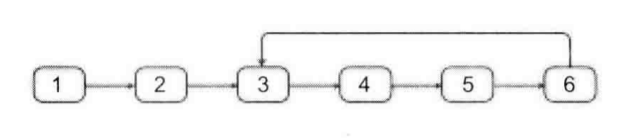
给定如上所示的链表:
[1, 2, 3, 4, 5, 6]
2
注意,这里的2表示编号是2的节点,节点编号从0开始。所以编号是2的节点就是val等于3的节点。
则输出环的入口节点3.
class Solution {
public:
ListNode *entryNodeOfLoop(ListNode *head)
{
ListNode *h1=head,*h2=head;
if(!head ||!head->next)
return NULL;
while(h1 && h2)
{
h1=h1->next;
h2=h2->next;
if(h2)
h2=h2->next;
else return NULL;
if(h1==h2)
{
h1=head;
while(h1!=h2)
{
h1=h1->next;
h2=h2->next;
}
return h1;
}
}
return NULL;
}
};
算法
(链表,快慢指针扫描) O(n)O(n)
本题的做法比较巧妙。
用两个指针 first,secondfirst,second 分别从起点开始走,firstfirst 每次走一步,secondsecond 每次走两步。
如果过程中 secondsecond 走到null,则说明不存在环。否则当 firstfirst 和 secondsecond 相遇后,让 firstfirst 返回起点,secondsecond 待在原地不动,然后两个指针每次分别走一步,当相遇时,相遇点就是环的入口。
证明:如上图所示,aa 是起点,bb 是环的入口,cc 是两个指针的第一次相遇点,abab 之间的距离是 xx,bcbc 之间的距离是 yy。
则当 firstfirst 走到 bb 时,由于 secondsecond 比 firstfirst 多走一倍的路,所以 secondsecond 已经从 bb 开始在环上走了 xx 步,可能多余1圈,距离 bb 还差 yy 步(这是因为第一次相遇点在 bb 之后 yy 步,我们让 firstfirst 退回 bb 点,则 secondsecond 会退 2y2y 步,也就是距离 bb 点还差 yy 步);所以 secondsecond 从 bb 点走 x+yx+y 步即可回到 bb 点,所以 secondsecond 从 cc 点开始走,走 xx 步即可恰好走到 bb 点,同时让 firstfirst 从头开始走,走 xx 步也恰好可以走到 bb 点。所以第二次相遇点就是 bb 点。
另外感谢@watay147提供的另一种思路,可以用公式来说明:a,b,c,x,ya,b,c,x,y 的含义同上,我们用 zz 表示从 cc 点顺时针走到 bb 的距离。则第一次相遇时 secondsecond 所走的距离是 x+(y+z)∗n+yx+(y+z)∗n+y, nn 表示圈数,同时 secondsecond 走过的距离是 firstfirst 的两倍,也就是 2(x+y)2(x+y),所以我们有 x+(y+z)∗n+y=2(x+y)x+(y+z)∗n+y=2(x+y),所以 x=(n−1)×(y+z)+zx=(n−1)×(y+z)+z。那么我们让 secondsecond 从 cc 点开始走,走 xx 步,会恰好走到 bb 点;让 firstfirst 从 aa 点开始走,走 xx 步,也会走到 bb 点。
时间复杂度
firstfirst 总共走了 2x+y2x+y 步,secondsecond 总共走了 2x+2y+x2x+2y+x 步,所以两个指针总共走了 5x+3y5x+3y 步。由于当第一次 firstfirst 走到 bb 点时,secondsecond 最多追一圈即可追上 firstfirst,所以 yy 小于环的长度,所以 x+yx+y 小于等于链表总长度。所以总时间复杂度是 O(n)O(n)。
C++ 代码
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
ListNode *entryNodeOfLoop(ListNode *head) {
if (!head || !head->next) return 0;
ListNode *first = head, *second = head;
while (first && second)
{
first = first->next;
second = second->next;
if (second) second = second->next;
else return 0;
if (first == second)
{
first = head;
while (first != second)
{
first = first->next;
second = second->next;
}
return first;
}
}
return 0;
}
};



